The equations of electromagnetism

  Maxwell's equations  for the electromagnetic field [ in units with ] are:

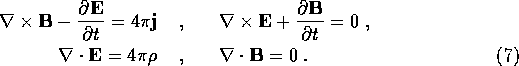
These equations show that one can have electromagnetic waves in a vacuum which travel with a speed , Thus light is a form of electromagnetic radiation.

 

Figure 1.2: James Clerk Maxwell

An Ether  was postulated as the medium which carries these waves [ i.e. the speed c is the speed with respect to the ether ] and naturally this was identified with the absolute space of Newton.

Attempts to measure the ether drift by Michelson and Morley in 1887 gave a null result, so effects like stellar aberration could not be due to the earth dragging the ether.

Another great problem was that Maxwell's equations did not appear to obey the principle of Galelian Relativity i.e. they were not invariant under the Galelian transformations. This means that in a moving space ship the electric and optical phenomena should be different from those in a stationary ship!!! Thus one could use for example optical phenomena to determine the speed of the ship.

One of the consequences of Maxwell's equations is that if there is a disturbance in the field such that light is generated, these electromagnetic waves go out in all directions equally and at the same speed c. Another consequence of the equations is that if the source of the disturbance is moving, the light emitted goes through space at the same speed c. This is analogous to the case of sound being likewise independent of the motion of the source. This independence of the motion of the source in the case of light brings up an interesting problem.

Suppose we are riding in a car that is going at a speed u, and light from the rear is going past the car with speed c. According to the Galelian transformations, the apparent speed of the passing light, as we measure it in the car, should not be c, but c-u. This means that by measuring the speed of the light going past the car, one could determine the absolute speed of the car. This is crazy because we already know that the laws of mechanics do not permit the measurement of absolute velocity.

• Something is wrong with the laws of Physics!!

At first people thought that it was Maxwell's equations that were at fault and they modified them so that they were invariant under the Galelian transformations; but this led to the prediction of new electrical phenomena which could not be found experimentally.

Then in 1903 Lorentz  made a remarkable and curious discovery. He found that when he applied the following transformations to Maxwell's equations

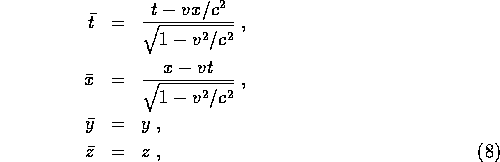
they remained invariant.

 

Figure 1.3: Hendrik Antoon Lorentz.

These are the famous Lorentz transformations and we will discuss them in more detail in section 4.